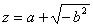
Trasformiamo la radice ennesima di un numero complesso in una somma di due radici ennesime
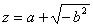
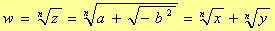
Per calcolare x e y, eleviamo a n entrambi i membri dell'equazione
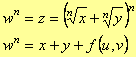
e applichiamo la tecnica adoperata per lo sviluppo delle potenze dei binomi
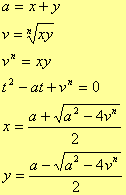
La radice ennesima di un numero complesso è data da
Ora è sufficiente calcolare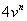
Secondo grado__________________________________________________________________
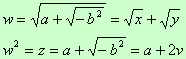
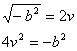
Quindi la radice quadrata di un numero complesso è data da
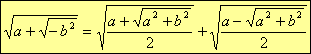
Il modulo di un numero complesso è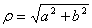 
quindi abbiamo
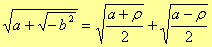
Terzo grado__________________________________________________________________
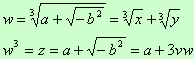
Da notare che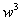
può essere semplificato perché è uguale al numero complesso z
Quindi la radice cubica di un numero complesso è data da
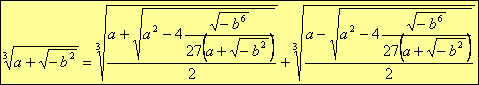
Da notare che
Se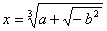 
e 
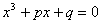
allora
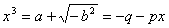
quindi
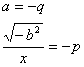
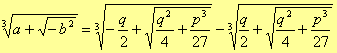
Che risolve l'equazione di terzo grado
Quarto grado__________________________________________________________________
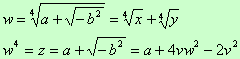
Da notare ch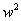e 
e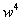 
possono essere semplificati perché sono uguali a radici conosciute di z
Quindi la radice quarta di un numero complesso è data da
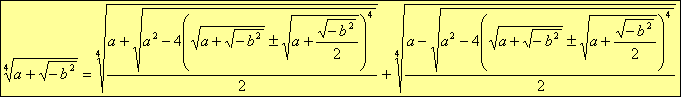
Quinto grado__________________________________________________________________
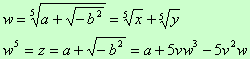
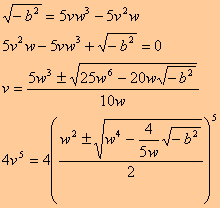
Essendo 5 un numero primo, si può semplificare w solo quando è elevata a 5 ed
a nessun'altra potenza, quindi a causa della presenza di w elevata alla prima,
alla seconda ed alla quarta potenza, non si riesce a calcolare il valore di
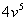per radicali.
Se non si riesce a calcolare la radice quinta di un numero complesso per radicali, non può esistere neanche la soluzione per radicali dell'equazione di 5° grado, perché presuppone la presenza della radice quinta di un numero complesso.
Sesto grado__________________________________________________________________
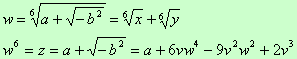
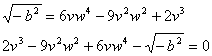
Siccom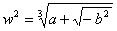e
e
sono radici cubiche di un numero complesso, possono essere calcolate con la con la relativa formula.