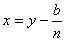 come nel prossimo esempio.
come nel prossimo esempio.Si intende risolvere le equazioni polinomiali di grado n, per mezzo della riduzione all'equazione depressa (mancante dell’esponente n-1) e poi con la riduzione ad una equazione di grado n-1.
Per ottenere l’equazione depressa è sufficiente impostare
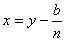 come nel prossimo esempio.
come nel prossimo esempio.
Equazione di secondo grado
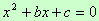
L’equazione di secondo grado si risolve semplicemente riducendo l’esponente n-1
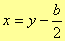
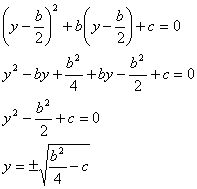
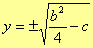
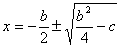
Equazione di terzo grado
L’equazione di terzo grado si risolve facendo entrambe le riduzioni
Partiamo dall’equazione depressa
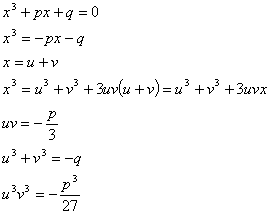
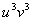 e
e 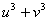 sono le radici dell’equazione di secondo grado
sono le radici dell’equazione di secondo grado
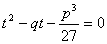 quindi
quindi
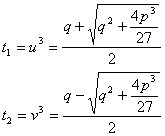
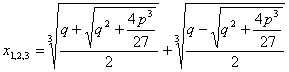
Equazione di quarto grado
L’equazione di quarto grado si risolve facendo entrambe le riduzioni
Partiamo dall’equazione depressa
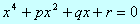
e consideriamo l’equazione di terzo grado
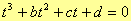 le cui soluzioni sono
le cui soluzioni sono
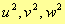
sappiamo che le relazioni tra le soluzioni dell’equazione ed i coefficienti sono le seguenti:
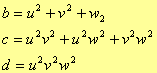
definiamo
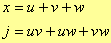
e calcoliamo
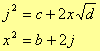
Ora, per trovare i coefficienti p,q,r, trasformiano
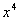 in un’equazione di secondo grado
in un’equazione di secondo grado
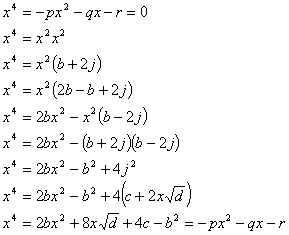
da cui si ricavano
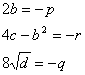
quindi

l’equazione di terzo grado è
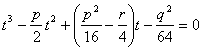
le cui radici sono
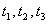
calcoliamo le radici dell’equazione di quarto grado che sono:
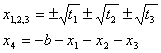
La soluzione dell’equazione di quinto grado non può essere calcolata con i soli radicali
Questo perché la soluzione presuppone la presenza della radice quinta di un numero complesso la quale non può essere espressa con i soli radicali, come ho dimostrato nello studio sulle radici dei numeri complessi.